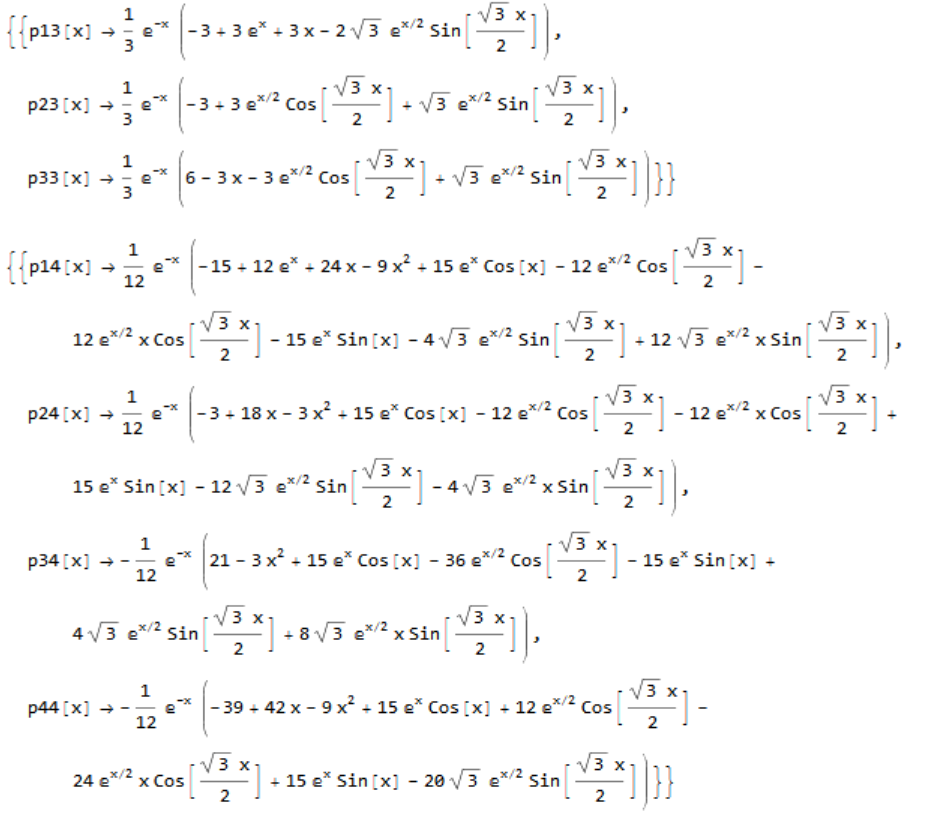[Above is a Mathematica-derived solution to the systems of equations described in the 4-player tournament described below]

Without loss of generality we can assume an arrow’s distance to the center of the target is U[0,1] distributed. Let P_j,k(x) denote the probability that Player j out of k in the current line will eventually win the game, given that the current best dart is at distance x.

In a 2-player archery tournament, we would have P_1,2(x) + P_2,2(x) = 1, P_1,2(0) = 0, and P_1,2(x) = ∫₀^x P_2,2(u) du. Taking derivatives of both sides in that last equation and substituing gives P‘_1,2(x) = −P_1,2(x). Solving gives P_1,2(x) = 1−e^−x.

In the 3-player version of the game, we get the following system of equations:

P_1,3(x) = ∫₀^x P_3,3(u) du

P_2,3(x) = (1 - x)P_1,2(x) + ∫₀^x P_1,3(u) du

P_1,3(x) + P_2,3(x) + P_3,3(x) = 1

P_1,3(0) = P_2,3(0) = 0.

And for the 4-player version we have the following:

P_1,4(x) = ∫₀^x P_4,4(u) du

P_2,4(x) = (1 - x)P_1,3(x) + ∫₀^x P_1,4(u) du

P_3,4(x) = (1 - x)P_2,3(x) + ∫₀^x P_2,4(u) du

P_1,4(x) + P_2,4(x) + P_3,4(x) + P_4,4(x) = 1

P_1,4(0) = P_2,4(0) = P_3,4(0) = 0.

In particular we have P_4,4(1) = (-5/4)*(cos(1) + sin(1)) + (1/2)*e^-1 + (e^-1/2)*(cos(sqrt(3)/2) + 5/sqrt(3)*sin(sqrt(3)/2)), or approximately 0.18343765086.

Congrats to this month’s solvers!