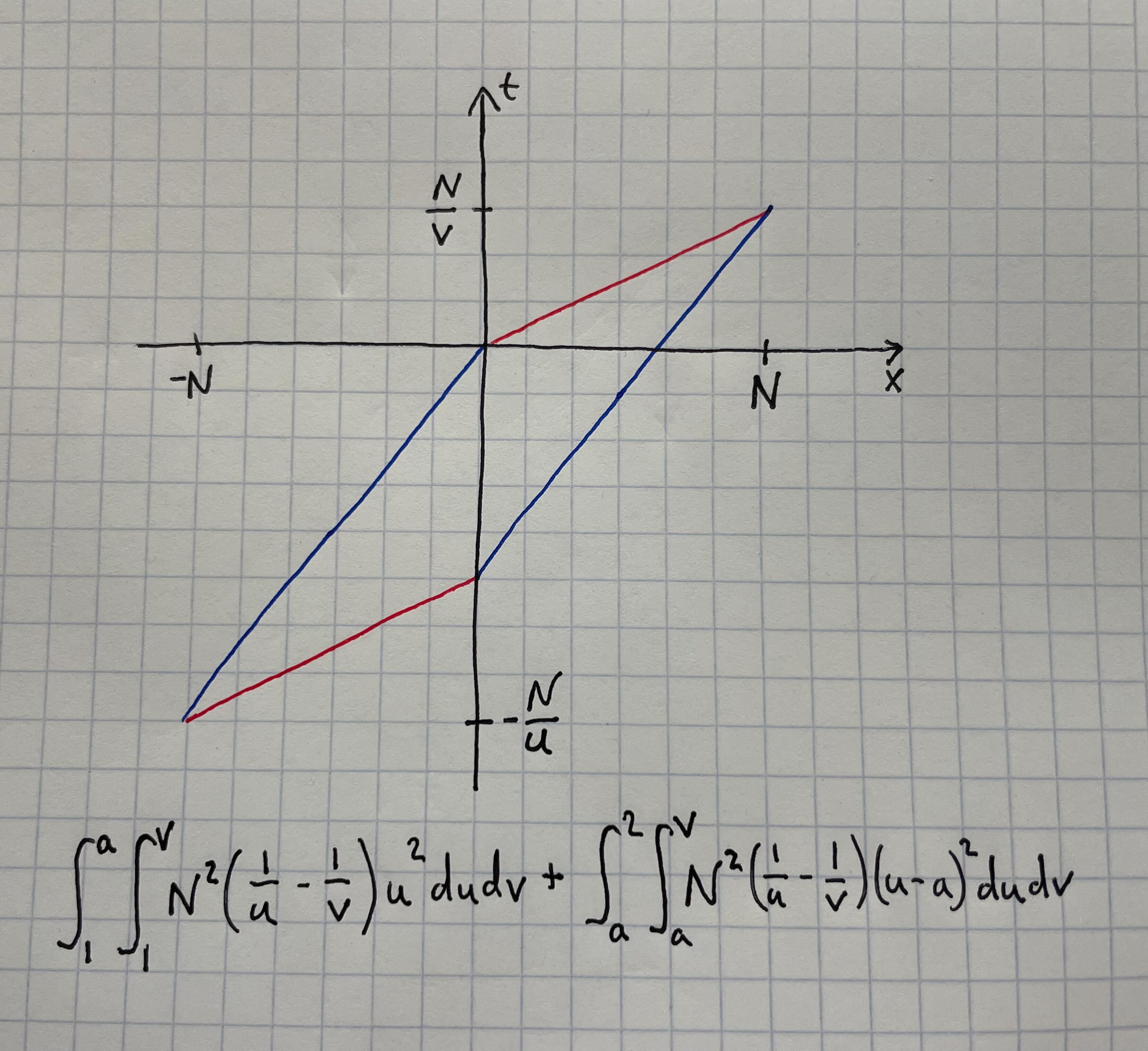The trickiest part of this probability puzzle is determining the relative base rates between cars of different speeds overtaking each other. The notes about how cars rarely meet and all trips are the same long length N (made precise by taking limits) implies that we can minimize the “first order term” of the cost of exactly two cars meeting and we can ignore the boundary effects of meeting near the beginning or end of one of the cars’ journeys. We know each car’s speed is uniformly chosen in [1,2], so to find the relative rates of overtaking we can integrate over two speeds being drawn and then consider the set of positions in distance and time (which we are also given as being uniform) that the slower car would’ve had to start at to be overtaken by the faster car.

So say the two speeds we select are u < v, and without loss of generality we fix the position of the car traveling v to enter the highway at (0, 0) (the first coordinate is in distance and the second is in time). Then the car will exit the highway at (N, N/v), and the starting positions of the u-speed car that need to be overtaken by the v-speed car are those within the pictured parallelogram (again we are ignoring weirdness along the boundary because it will go to zero in the limit). A few different methods can compute the area of this parallelogram to be N²(1/u - 1/v). There are other ways to reason out this base rate but I like drawing parallelograms.

Now we must compute the cost of each overtake as a function of the speed of the overtaken car, it turns out to be in proportion to the square of the difference between u and the speed the car must reduce to. This implies we are trying to choose a to minimize the sum of the integrals pictured. The first integral is the cost of reducing speed from the slow lane to zero and the second integral is the cost of reducing speed from the fast lane to the slow lane. The N² factors out and can be ignored, and some fundamental theorem of calculus and integration computing can get to an expression in a whose solution is 1.1771414168…

Congrats to all the solvers able to find the optimal speed limit!