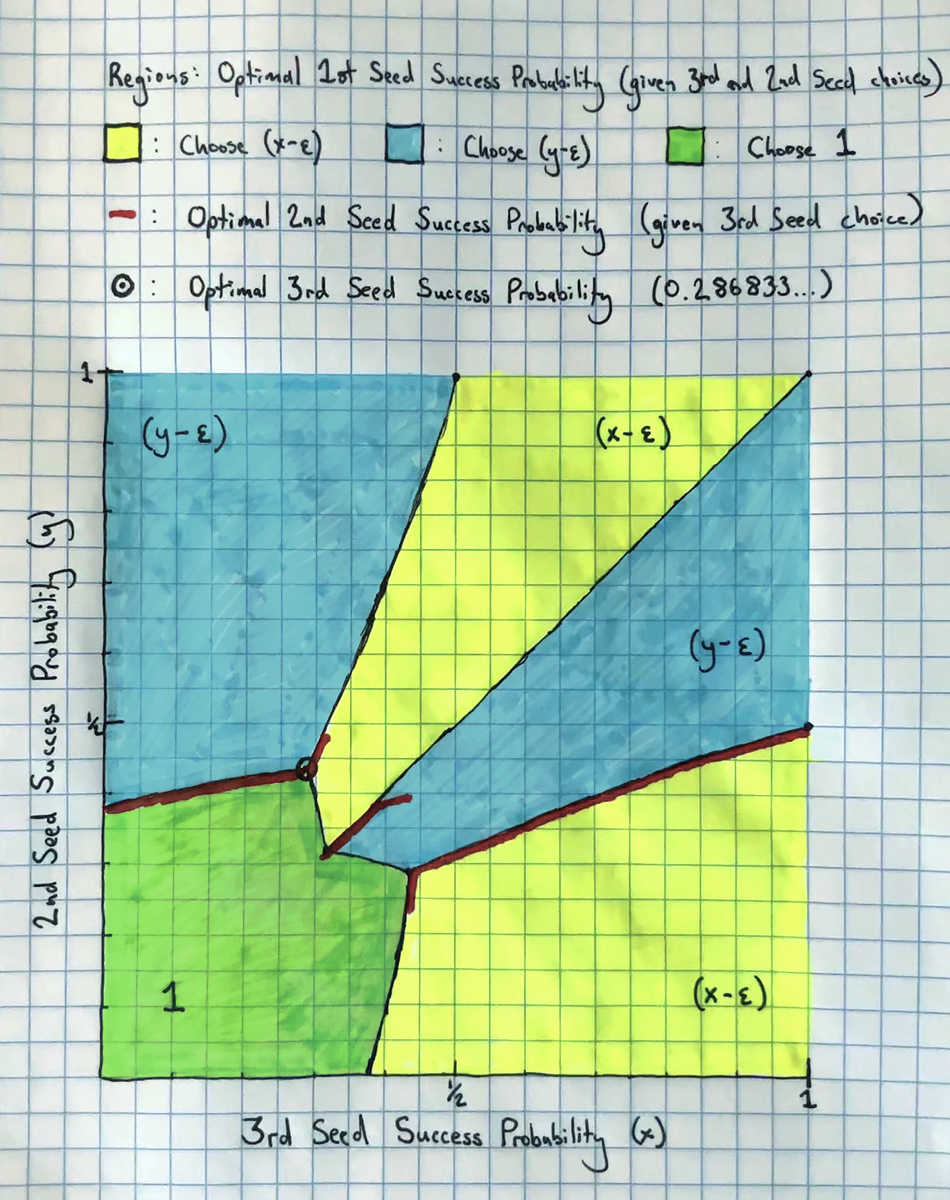
To solve this problem, it’s best to work backwards from the decision of the 1st seed, who selects their attempted weight last. We will work with the 1st, 2nd, and 3rd seed’s probability of successfully lifting their selected weights (we can ignore the actual weight amounts and just phrase everything in terms of these probabilities).

So the 1st seed knows the probability that the 3rd seed will successfully lift (call it x), and the probability that the 2nd seed will succeed (y). Given the 1st seed’s lift will only be judged against the other two lifts, there are three possible strategies to consider for the 1st seed, any other strategy is dominated by one of these:

1. lift an arbitrarily small amount more than the 3rd seed, to have (x-ε) chance of success,
2. lift an arbitrarily small amount more than the 2nd seed, to have (y-ε) chance of success, or
3. lift zero weight with success probability 1.

Without loss of generality, we can assume x<y and compute the curves that separate the regions where each of these strategies is optimal by setting their payoffs equal. The probability of a 1st seed victory of the respective strategies, as ε -> 0+, are

1. x/(1-(1-x)²(1-y))
2. (1-x)y/(1-(1-x)(1-y)²)
3. (1-x)(1-y)

Setting these pairwise equal divides the space into three regions. We can reflect this about the line x=y and get what the 1st seed will do in every circumstance (represented by the yellow, blue, and green regions in the graph). We then can optimize the 2nd seed’s choice conditional on the 3rd seed’s selection (represented by the red line in the graph).

Remarkably, the function for the 2nd seed’s optimal probability of lifting (y), dependent on x, is piecewise smooth with six different pieces and two jump discontinuities. Once we have these we can detect the optimal choice for the 3rd seed (the circled point on the graph). This ends up being 0.286833… which is one of the points of triple intersection of the three strategies listed above. That is, it turns out to be in the best interest of the 3rd seed to “collaborate” with the 2nd seed to make the 1st seed indifferent between the three strategies listed¹. Unfortunately for the 3rd seed, the only way to get the 2nd seed to cooperate with this plan is to accept the worse of the two positions in this triple-intersection point. So the selections will be:

x = 0.286833…

y = 0.436041…

z = 1

Which leads to the following probabilities of winning:

3rd seed: 0.286833…

2nd seed: 0.310970…

1st seed: 0.402197…

[1] While the 1st seed is indifferent between the three idealized strategies, only one of them is achievable because the other two strategies are limiting as ε -> 0. So we can assume that if the 3rd seed and 2nd seed exactly measured their weights to perfect precision, the 1st seed would choose the zero weight lift.

Congrats to this month’s solvers who successfully found the answer!