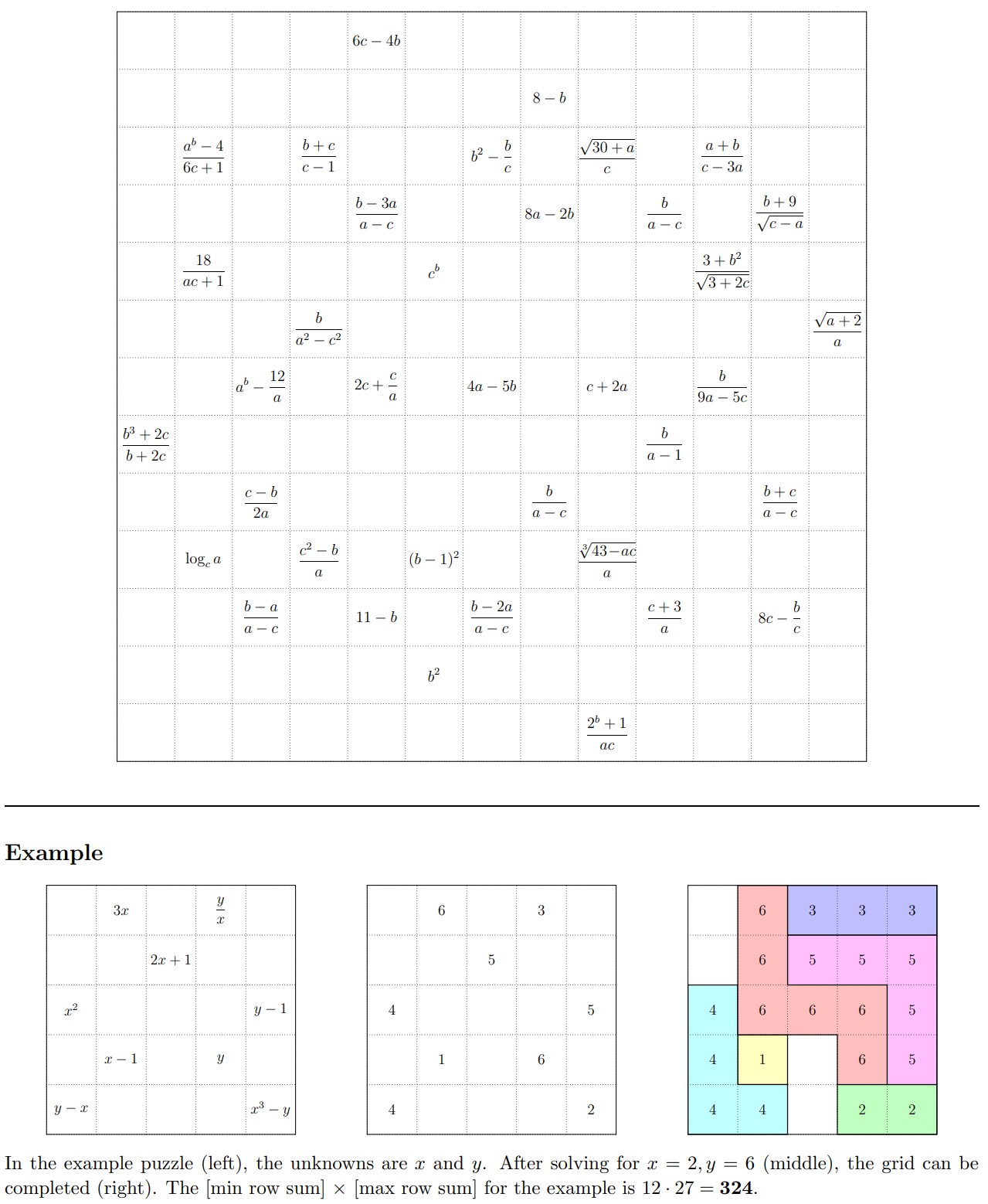
Place positive integers in some of the cells above, so that the grid contains one 1, two 2’s, three 3’s, and so on, up to N N’s. (For some N.)

For any integer K in the grid, the cells labeled K must form an orthogonally connected region (a “K-omino”). Furthermore, for each K > 1 the K-omino must “contain” the shape formed by the (K−1)’s. (Rotations and reflections are allowed.)

Some of the cells have been labeled, but unlike our previous Subtiles, we have used variables to obscure those values. (As in the example, at the bottom.)

After completing the grid, compute, in each row, the sum of the labeled cells. The answer to this puzzle is the product of the maximum and minimum row sums.